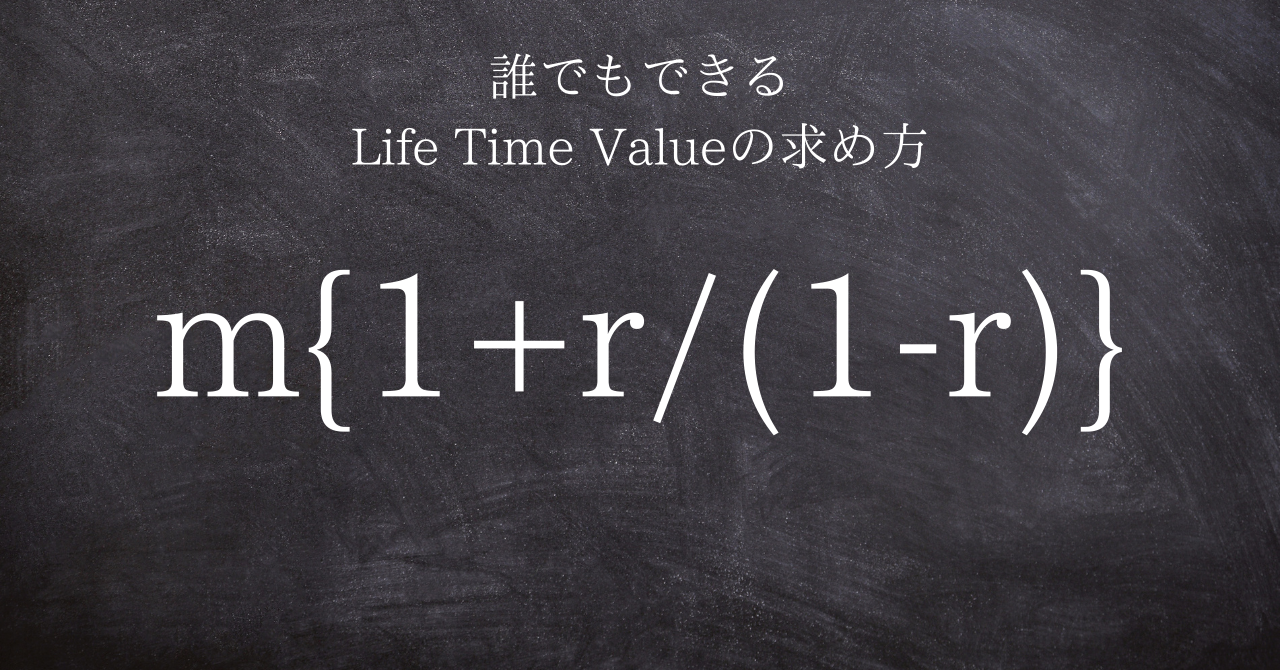
LTV(Life Time Value)とは。

マーケティング業務をしている方であればおなじみのLTV(Life Time Value)。

LTVは「ある顧客が、取引を開始してから自社に対してどれだけ利益をもたらしたか、収益の総額を算出するための指標。」といえます。

施策を一時的なスパンで評価するのではなく、長期的に、言い換えると顧客の生涯にどのような影響を与えたかを測るものです。

しかし、実際にこの指標を実務で使えている方はそう多くないのではないかと思います。

何故か？

それは計算方法がわからない。厳密には計算方法が使えないからだと思います。

そこで本記事では、簡単に計算して実務で使えるLTVの計算方法についてご紹介します。

一般的なLTVの計算方法

一般にLTVの計算式は以下で説明されている事が多いです。

しかし。実際にこの方法でLTVは計算できるのでしょうか？

難しいのではないでしょうか。

なぜなら、【顧客期間】を算出するのは不可能だからです。

顧客期間とは「どのくらいの期間、顧客であるか？」を指している変数だと思いますが、それって出せるのでしょうか？

ある人が顧客になってから、「いつまで顧客か？」って、死ぬまでその人を追わないと明確に言えないですよね。なぜなら、一回買って、途中で辞めてもう1回買うかもしれないからです。

そう考えると、半永久的に顧客期間を追うのは不可能と思うわけです。

そこで今回は誰でもざっくりとLTVを算出できる計算式をご紹介します。

それがこちらです。

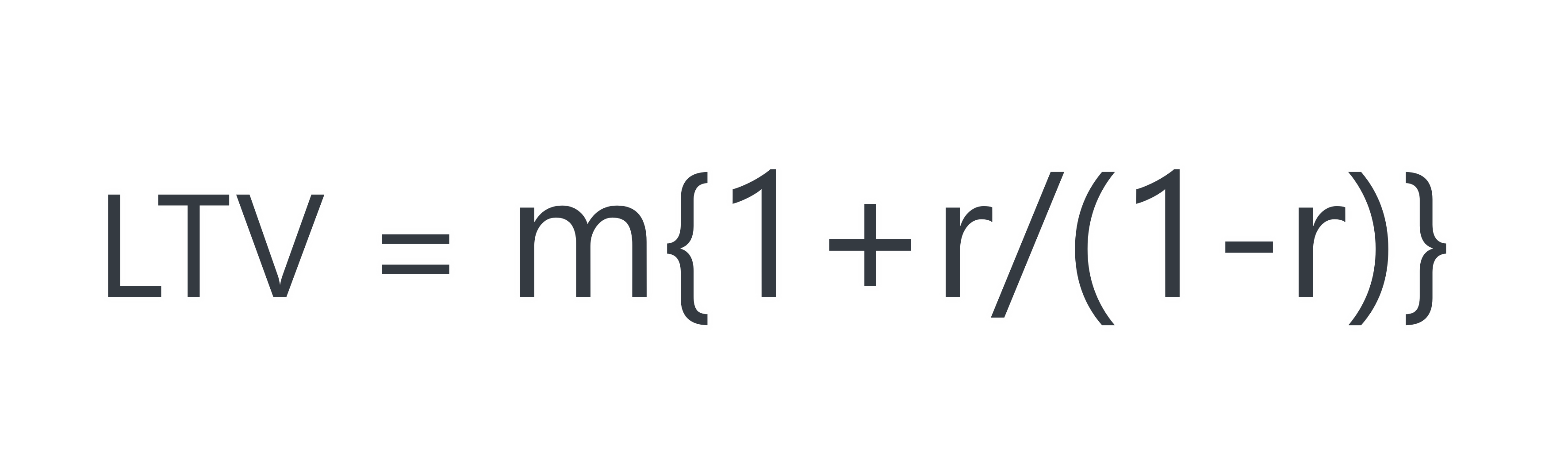
今回ご紹介するLTVの計算方法

そこで今回は誰でもざっくりとLTVを算出できる計算式をご紹介します。

それがこちらです。

なんか複雑そうですね…

でもよく考えると「単純なのに、理論的で、使いやすい」と思うので、ぜひ最後までご覧ください！

計算に使う数値

まず今回使う数値は

・ｍ＝一定期間の顧客1人当たりの利益

と

・ｒ＝顧客維持率

です。

ーーーーーーーーーーーーーーーーーーーーーーーーーー

■ｍ＝一定期間の顧客1人当たりの利益

例えば、一定期間を1年と考えて、1年間にどのくらい顧客は利益を生むかな？と考えます。だいたい1年で1万円だとすれば、今回は1万円と設定しましょう。

■ｒ＝顧客維持率

次に、顧客維持率ですが、こちらは同じく一定期間である1年間でどのくらい顧客が残るかという数値です。例えば、今年買った顧客が1年後に50%くらいの確率で買うと想定されれば、50%と設定します。

ーーーーーーーーーーーーーーーーーーーーーーーーーー

用意する数値は以上です。

これくらいであれば、用意できそうではないでしょうか？

例えばを考えてみる

とある企業のお客さんは

・平均的に1年間に100万円の利益をもたらす。

・平均的に1年間で60%くらいは翌年度も利用してくれ、残り40%は離反する。

とした場合、

LTV＝100万円｛1＋60%/(1-60%)}=400万円

という事で、400万円になる。

ここからはなぜ前述した計算式になるのかの証明です。

「細かい計算は面倒」という方は、信じて、先の2つの数値を計算式に当てはめて使ってみてください。

「理解しないと使えないよ！」という方は以下計算手順をご確認ください。

それがこちらです。

計算式の証明

まず今回使う数値は改めてですが、こちらです。

次に毎年の利益を確認します。こちらです。

1年目の利益はシンプルに m (一定期間の顧客1人当たりの利益)だけですね。例えば、1万円です。

2年目の利益はそこに r (顧客維持率)を掛け合わせます。rを50%とするなら、1万円×50%＝5,000円です。

3年目の利益は、2年の利益にさらに r を掛け合わせます。なぜなら、毎年維持率は50％で推移するので、50%×50%で25%になるからです。

先ほどの例でいうと、1万円×25%で、2,500円です。

4年目の利益は、3年目の利益にさらにrを掛け合わせて、1,250円です。

5年目以降も同じように計算します。

そしてそれらを足し合わせます。こちらです。

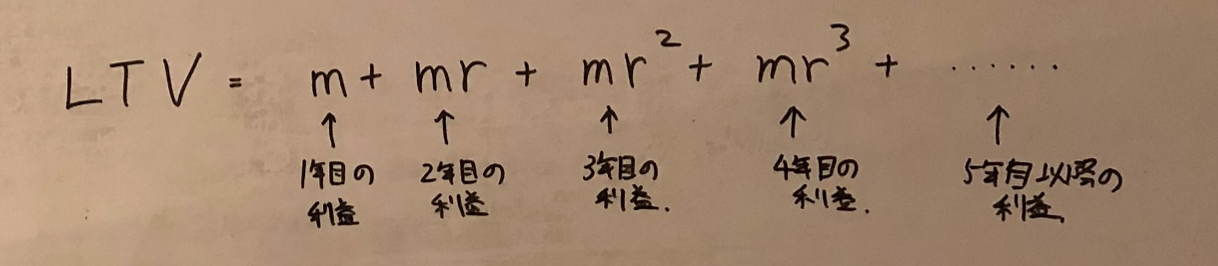
これがLTVの求め方です。

省略していますが、もちろん5年目以降も同じように足し合わせていきます。

ここで1つ留意しておきたいのは、5年目以降は無限大にずっと足し合わせていく式になっています。つまり顧客期間を無限としてとらえています。「顧客期間を無限にしてよいのか？」という疑問が生まれるかと思いますが、これの理由は最後に記述します。しかし、無限にしているからこそ実践的に簡単に使えるのです。

そして、その後は以下のように計算をしていきます。(ここからはこの式を変形していきます。)

最終的には、無限で表現していたSが打ち消され、簡単な式に変形する事ができました。

この式の使いやすさ

そして、この式の使いやすい部分、それは以下です。

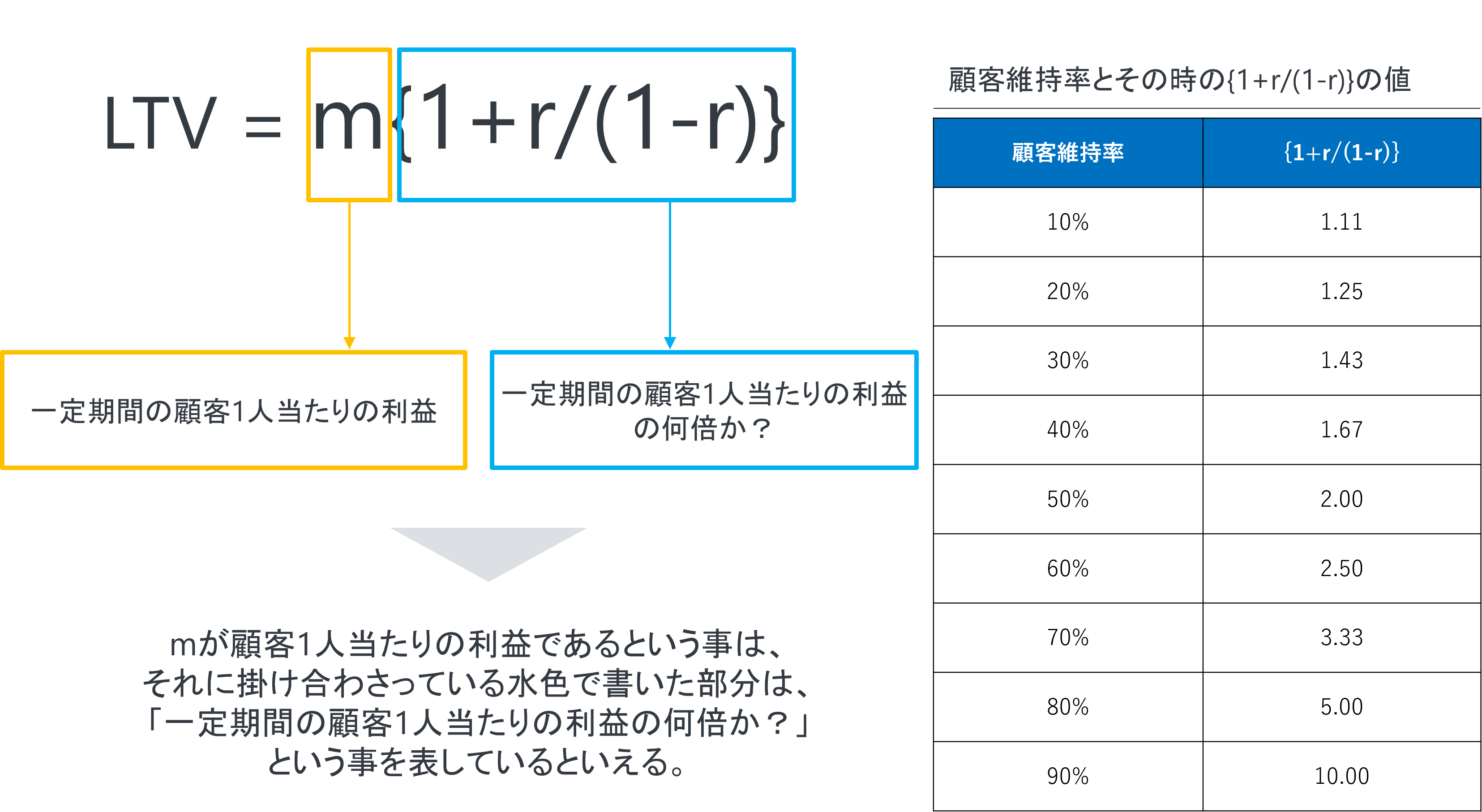
この式を見ていただくと、LTVは【ｍ】と【{1+r/(1-r)}】という部分に分かれていると思います。

【ｍ】は「一定期間の顧客1人当たりの利益」なので、【{1+r/(1-r)}】はその倍数になるわけです。

画像の右側の表を見ていただきたいのですが、例えば、【ｒ】が50%であれば、【{1+r/(1-r)}】は2.00になっています。

つまり、ｍ＝1万円だとすると、

LTV＝m×{1+r/(1-r)}なので、1万円×2.00＝2万円となるわけです。

どうでしょうか。簡単に出せたのではないでしょうか。

もしLTVが2万円が低い！と思われる方は、それは維持率の問題なので、例えば、90%まで上げると倍数は10倍(LTVは10万円)まで高くなります。

もちろん「一定期間の顧客1人当たりの利益」や「維持率」は人によって変わるので、おおざっぱな計算になりますが、それは【顧客単価×顧客頻度×顧客期間】でも同じですし、それよりも簡単に出せるようになるのではないかと思います。

顧客期間を無限にしている説明

最後に、顧客を無限としている説明ですが、以下です。

① は【顧客単価×顧客頻度×顧客期間】が無理だから、他の方法を考えました。という説明です。

ーーーーーーーーーーーー

② は以下をご覧ください。

仮に一定期間(今回は1年間)の顧客の利益が1万円、維持率が50%の場合、利益が10年目には20円になっています。これは「顧客が毎年50％ずつ残る」、逆に言えば「50％ずつ顧客は減っていく」ので、減った顧客の利益は0円になるわけです。その分も加味されているので、期間を無限として考えても、長くなればなるほど利益額は減るので、そこまで問題ないでしょう。という考え方です。

ーーーーーーーーーーーー

③これは②で納得できなかった向けへの説明ですが、この無限という考え方は実は企業価値を計算する時にも用いられるものです。

企業買収する際などに、企業価値を測るのですが、その際に「企業の活動は永久的」と考えて、期間を無限として将来の利益を算出します。その際にも【割引率】という考え方を使って、今回の維持率と同じように「徐々に利益は少なくなるから問題ないよね。」という考え方を使っています。今回の計算式もその考え方を応用して作られています。

最後に

いかがだったでしょうか？この計算式だと、指標も使いやすく、ＬＴＶも簡単に計算できるのではないかと思います。（なんなら感覚で、1年で利益は○○円、維持率は○○％と考えてもよいと思っています。）

ちなみに、お金の時間的価値も考慮して、割引率をこの式に入れて使う事もできます。